我们所有人的生活都受到有限空间和有限时间的限制,因此常常需要作出一些取舍。从小到大,我们心中可能有很多想法和目标,无论是取得好的学习成绩还是升职加薪,也有可能是追到心仪的女孩或学会一个新的技能。但实际上,实现目标获得最优解,不只是我们生活中才有的问题,数学家也常常面临这些问题,在数学上获得最优解的问题称之为优化问题,而他们解决问题的思路可以给我们很大启发 。
优化设计问题有三大要素,分别是设计变量、约束条件和目标函数。我们以打牌为例,我们的目标是赢得牌局的胜利,这对应的是目标函数。打牌有一定限制规则,不能随便乱打,这就相当于约束条件。我们手里每个人拿什么牌可以看做一种输入数据,这对应的是设计变量。
在数学上优化理论主要研究的是如何才能快速达到自己目标的科学,这里面就涉及到很多种优化算法。在我们谈具体优化方法之前,我们需要先明确两个点:设计变量和约束条件。
设计变量告诉我们只有正确的输入,才有可能对应正确的输出。比如说你每天都在学习英语,没有在编程技术上有任何的学习输入,却想要提高自己计算机水平,这基本上是无法实现的。约束条件束缚住我们可以做事情的范围,比如说家庭财富并不富裕,还想过纸醉金迷的生活,往往没有办法实现。
下面我们来谈谈优化算法,不同的优化算法会有不同的时间目标时间,所以我们说磨刀不误砍柴工,打磨做事的方法,找到更优策略总是很重要的事情。这里,我想讨论的是一个选择问题。
很多时候,我们实现目标可以有很多选择。特别是当目标比较遥远,不清晰明确的时候。比如你今天中午想要吃饱肚子,A、B、C三家餐馆,没有太多需要纠结的地方。当你的目标是十年之后一年可以挣100万的时候,可以成为一名技术专家,可以自己创业,或者合伙承包项目等等。选择的可能性太多,你也不知道自己的选择是否正确,是否一定能够走通,常常就会迷茫,不知道该如何做出选择。
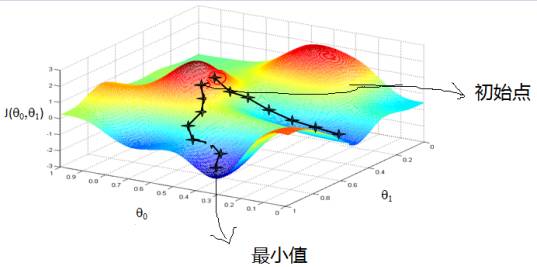
如上图所示,想要达到目标位置(最小值)有多种选择路径。于是就有可能出现局部最优的情况。也就是俗称的短视,只看到眼前的最优解,可能并不是长远来看的最优解。
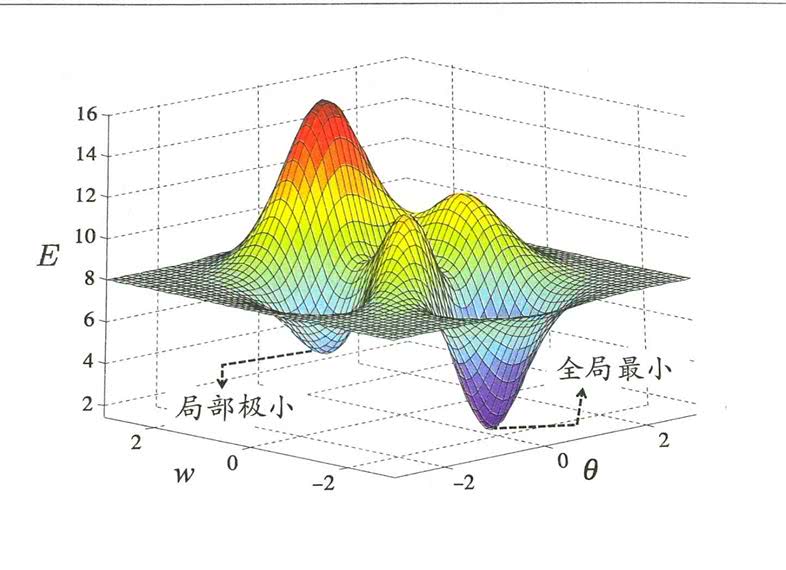
如何才能避免短视问题呢?从数学上来说,越高纬的空间越不容易陷入局部最优,比如说我们以一维为例
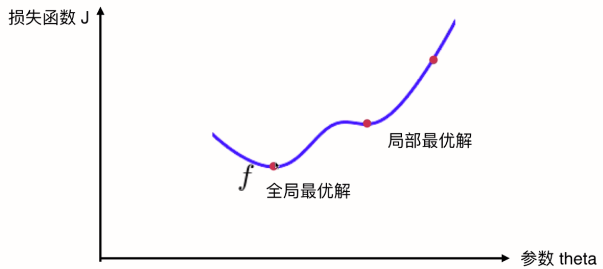
陷入局部最优解之后,两边的值都比局部极小值要高,所以很容易就陷入局部最优走不到全局最优的位置了。但是,如果把维度扩展为二维呢?在上图的一维的位置局部最优,新扩展的第二个维度没准就可以走出来,达到全局最优。可以想象,维度越高越不容易陷入局部最优。
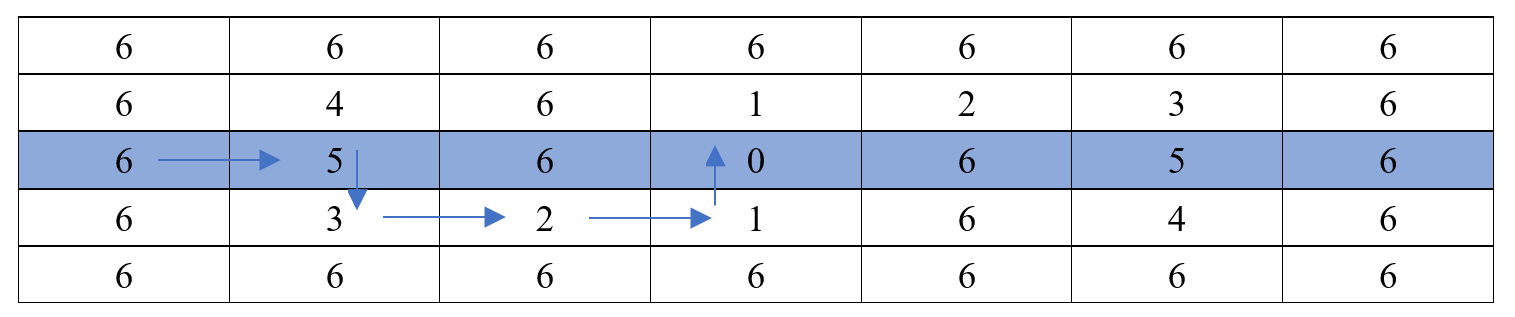
什么意思呢,用数字阵列举个例子。我们假设地形是一个复杂地形是一个一维函数。不同的数值表示地形的海拔高度。其中0是最小的海拔高度,其次是5。无论从哪一边下山,如果视野不够开阔的话,都会困在5个这个局部极小值里,以为5就是最低的海拔高度了。

但是,如果将这个地形叠加为二维函数,仍用数字表示海拔高度,我们可以看到,无论从哪一边开始下山,每走一步,当在一维函数中走到“局部极小值”5以后,在另外一个维度函数中,则可以走到更低的海拔,直到到达“全局最小值”0。同样的,维度越多,在某一个维度达到“局部最小值”后,可以选择其他维度和路径就越多,因此被困在“局部最小值”的概率就越低。
这给我们什么启示呢?眼界,格局很重要。我们思考层面越高,思考问题的维度越高,往往从一个角度看起来棘手的问题,从另外一个角度就可以解决。提高见识很重要。
扩展思考维度的效果是怎么样呢?我来举一个例子。
| 别人都是正确的 | 别人都是错误的 | |
|---|---|---|
| 你是正确的 | ||
| 你是错误的 |
正确本身,其实可能没有价值。
若你是正确的,与此同时,别人也是正确的,那“正确”本身的价值并不大。若你是错误的,别人都是正确的,那会是一个很可怕的局面。若你是正确的,别人都是错误的,这时“你的正确”才具备很大价值。
英语中有一个词叫“contraction”,原意是指股市中那些和别人做法极不相同的人。“特立独行”本身的价值和“正确”本身的价值一样,并不算大,但“特立独行且正确”的价值就相当巨大了。
我们从两个维度思考,结果就相当清晰了。
你的正确程度越大,与此同时,不认同你的人越多,你的价值就越大。若你很正确,但与此同时,所有人都很正确,那你的价值其实等于零。
例如,现在你看好VR/AR,大家也看好VR/AR,你去做这方面创业,其实胜算并不高。因为大家都看好,都想做,所以,谁的资源多,谁就最有可能成功,而“你看对了”这件事本身不会给你带来哪怕多一点点想相对优势——在“正确程度”这个维度上,你不一定比别人“更正确”,没准别人在“正确程度”上还超过你不少。